গণিত অলিম্পিয়াডের আদ্যোপান্ত – প্রাইমারি ক্যাটাগরির প্রস্তুতি

গণিত উৎসবে প্রাইমারি ক্যাটাগরি বলতে আসলে তৃতীয়-পঞ্চম শ্রেণির শিক্ষার্থীদের বুঝায়। বেশীরভাগ ক্ষেত্রে শিক্ষার্থী কিংবা অভিভাবকেরা যে প্রশ্নগুলো করে থাকে সেগুলো এরকম: 
আমি তৃতীয় বা পঞ্চম শ্রেণিতে পড়ছি, প্রথমবারের মত গণিত অলিম্পিয়াডে অংশগ্রহণ করবো-

• কিভাবে প্রস্তুতি নিতে পারি?
• কোন বই পড়লে ভালো হবে?
• কবে থেকে প্রস্তুতি শুরু করবো?

আমরা ইতোমধ্যে বলেছি যে, মোটাদাগে অলিম্পিয়াডের প্রশ্নগুলো সংখ্যাতত্ত্ব, গণনা, বীজগণিত, জ্যামিতি, যুক্তি- এই পাঁচটি বিষয় থেকেই হয়ে থাকে। কয়েকটি প্রশ্ন নিয়ে আলোচনা করলে ব্যাপারটা বোঝা সহজ হবে। আজকের লিখা মূলত প্রাথমিক ক্যাটাগরির কিছু সমস্যা সমাধান ও প্রস্তুতি নিয়ে।

প্রাথমিকের শিক্ষার্থীরা তাদের পাঠ্যবই থেকে সংখ্যার স্থানীয় মান, সংখ্যার বিভিন্ন গাণিতিক প্রক্রিয়া (যেমন: যোগ, বিয়োগ, গুণ, ভাগ) এসব সম্পর্কে জানতে পারে। এরপর, ধাপে ধাপে তারা গড়, ঐকিক নিয়ম, শতকরা, লাভ- ক্ষতি নিয়ে ধারণা লাভ করে যা মূলত সংখ্যার বিভিন্ন গাণিতিক প্রক্রিয়ার ভিন্ন ভিন্ন রূপ। গণিত অলিম্পিয়াডে সংখ্যা সংক্রান্ত অনেক ধরণের সমস্যা থাকে যেমন: উৎপাদক, লসাগু, গসাগু, জোড়, বিজোড়, বিভাজ্যতা ইত্যাদি। উদাহরণ হিসেবে নিচের এই সমস্যাটি দেখা যাক-

“ফুয়াদের কাছে কিছু আপেল আপেল রয়েছে, 100 টিরও বেশি নয়, 10 টিরও কম নয়। যদি সে একটি  আপেল সরিয়ে নেয়, তাহলে অবশিষ্ট আপেল দুইজনের মাঝে সমানভাবে ভাগ করা যেতে পারে। আবার, যদি সে আরেকটি আপেল যোগ করে, তাহলে আপেলগুলো তিনজনের মধ্যে সমানভাবে ভাগ করা যেতে পারে। ফুয়াদের কাছে থাকা আপেলের সম্ভাব্য পরিমাণ কত ভিন্ন রকমের হতে পারে?”

এখানে প্রশ্ন দেখে বোঝা যাচ্ছে যে, ফুয়াদের কাছে অবশ্যই বিজোড় সংখ্যক আপেল আছে! কারণ একটি আপেল সরিয়ে রাখার পর অবশিষ্ট আপেল দুই জনের মাঝে সমান ভাবে ভাগ করে দেয়া সম্ভব হয়, শুরুতে জোড় সংখ্যক আপেল থাকলে এটি সম্ভব হতো না। কাজেই, এ তথ্য অনুযায়ী উত্তর হতে পারে 11, 13, 15 ইত্যাদি। আবার, যে পরিমাণ আপেল আছে, তার সাথে আরেকটি আপেল যোগ করলে সেগুলো তিন জনকে সমান ভাগে ভাগ করে দেয়া যাবে। অর্থাৎ, ফুয়াদের কাছে যে পরিমাণ আপেল আছে তার সাথে আরেকটি আপেল যোগ করলে তা তিন দ্বারা বিভাজ্য বা তিনের গুণিতক সংখ্যা হবে! তিনের গুণিতক সংখ্যাগুলো আমরা জানি- 12, 15, 18, 21… এসব। এই দুই তথ্য থেকে আমরা কিন্তু সহজেই সমস্যাটি সমাধান করতে পারি।

আরেকটি সমস্যা নিয়ে আমরা ভেবে দেখতে পারি-
“একটি ক্লাসে এমন সংখ্যক শিক্ষার্থী আছে যে, তারা 5 টি বেঞ্চেও বসলেও প্রতি বেঞ্চে সমান সংখ্যক শিক্ষার্থী বসতে পারে। আবার, 8 টি বেঞ্চে বসলেও প্রতি বেঞ্চে সমান সংখ্যক শিক্ষার্থী বসতে পারে। ঐ ক্লাসে কমপক্ষে কতজন শিক্ষার্থী আছে?”

এই সমস্যা সমাধানের ক্ষেত্রে আমরা যদি 5 এর গুণিতক এবং 8 এর গুণিতকের একটি তালিকা করি, তাহলেই বুঝতে পারবো উত্তর কেমন হতে পারে। (সঠিক উত্তর বের করার দায়িত্ব পাঠকের হাতে ছেড়ে দিলাম!) 

অলিম্পিয়াডের কিছু সমস্যা আছে যেগুলো একটু ব্যতিক্রম, পড়ে তৎক্ষণাৎ বোঝা যায় না কিভাবে সমস্যাটি সমাধান করা যেতে পারে। এক্ষেত্রে একটা ভালো বুদ্ধি হলো উল্টো পথে হাঁটা বা ব্যাকট্রাকিং! অনেক কঠিন একটা শব্দ ব্যবহার করে ফেললাম! ব্যাপারটা আসলে এতো কঠিন না, নিচের সমস্যাটি দেখলেই বোঝা যাবে-

“তুমি 2 সংখ্যাটা দিয়ে শুরু কর। প্রতি ধাপে হয় তুমি তোমার কাছে থাকা সংখ্যাটার সাথে এক যোগ করতে
পারো অথবা তিন গুণ করতে পারো। তুমি 31 সংখ্যাটাতে যেতে চাও। সর্বনিম্ন কয়টা ধাপে তুমি এই কাজটা করতে পারবে?”

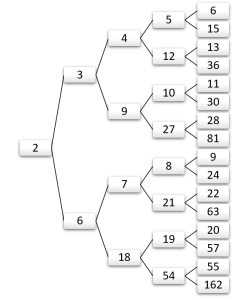ছবি: ২ থেকে পরবর্তী ধাপে যাওয়ার বিভিন্ন উপায়

এখানে, প্রশ্ন অনুযায়ী 2 থেকে শুরু করলে কিন্তু 3 কিংবা 6 এই দুইটাতে যাওয়া সম্ভব। এভাবে চিন্তা করলে অনেক গুলো সংখ্যাতে যাওয়া যায়। আরেকভাবেও কিন্তু চিন্তা করা যেতে পারে; আমরা শুরু করবো 31 থেকে, প্রতি ধাপে 1 বিয়োগ কিংবা 3 দিয়ে ভাগ করার চেষ্টা করে 2 সংখ্যাটি পাওয়ার চেষ্টা করবো, এভাবে উত্তরে পৌঁছানো
সম্ভব হবে। (সঠিক উত্তর তাহলে কত হবে? এটাও পাঠকের হাতে ছেড়ে দিলাম!) 

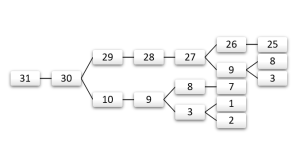ছবি: ব্যাকট্র্যাকিং করে ৩১ থেকে ২ এ পৌঁছানোর উপায়

আশা করছি, এই লিখা থেকে প্রাথমিক ক্যাটাগরির প্রস্তুতি নিয়ে একটা ভালো ধারণা পাওয়া গেছে। আসলে অলিম্পিয়াডে ভালো করতে হলে বেশি বেশি সমস্যা সমাধানের কোন বিকল্প নেই। আমাদের ওয়েবসাইটে সাপ্তাহিক সমস্যা বিভাগে বিভিন্ন গাণিতিক সমস্যা দেয়া হয়, কেউ চাইলে এগুলো নিয়মিত সমাধান করতে পারে। 

পরবর্তী লিখাতে আমরা জুনিয়র ক্যাটাগরির প্রস্তুতি নিয়ে লিখবো। সে পর্যন্ত বাংলার ম্যাথের সাথে থাকুন, গণিতের সাথে থাকুন।

(গণিত অলিম্পিয়াড সিরিজের পর্ব-১ পড়তে এখানে ক্লিক করুন,  পর্ব-২ পড়তে এখানে ক্লিক করুন)